Python skripte

Kazalo

1. Premica po metodi najmanjših kvadratov
2. Predstavitev z histogramom
3. Premica po metodi najmanjših kvadratov z upoštevanjem napak

1. Primer iskanja koeficientov premice po metodi najmanjših kvadratov

Skripta v pythonu poišče koeficiente premice in napake koeficientov. Podatki se nahajajo v datoteki test.txt v dveh stolpcih. V prvem stolpcu je x, v drugem je y.

from scipy import polyval,sqrt,stats
import matplotlib.pyplot as plt
import numpy as np

data=np.loadtxt("test.txt")
x=data[:,0]
y=data[:,1]

slope, intercept, r, prob2, see = stats.linregress(x, y)
mx = x.mean()
sx2 = ((x-mx)**2).sum()
sd_intercept = see * sqrt(1./len(x) + mx*mx/sx2)
sd_slope = see * sqrt(1./sx2)

print "intercept:",intercept," error:",sd_intercept
print "slope:",slope," error:",sd_slope

yr=polyval([slope,intercept],x)

#matplotlib ploting
plt.title('Linear Regression Example')
plt.plot(x,y,'go')
plt.plot(x,yr,'--')
plt.legend(['measurement','fit'])
plt.ylabel('y label (units)')
plt.xlabel('x label (units)')
plt.axis([0,100,0,1000])
plt.show()

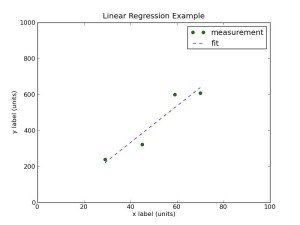
Rezultat zgornje skripte je prikazan na sliki (levo). matplotlib ponuja še nešteto izboljšav slike. Skripta izpiše v terminalu vrednosti koeficientov in njihove napake:

intercept: -73.7  error: 4.0
slope: 10.17  error: 0.075

Statistično gledano trdimo, da je koeficient naklona 10.17 ± 0.08 ter koeficient preseka -74 ± 4.

Nazaj na prejšnjo stran

---

2. Primer predstavitve podatkov v obliki histograma in normalne porazdelitve

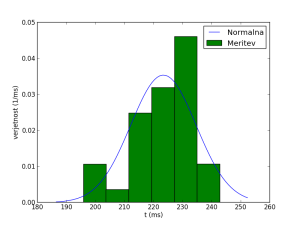
Spodnja skripta (avtor M.Živec), predstavi podatke iz datoteke text.txt, ki so podani v enem stolpcu, v obliki histograma. Na to sliko doda še normalno porazdelitev. Sredina in širina normalne krivulje sta povprečna vrednost in varianca vzorca.

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.mlab as mlab
from scipy.stats import norm
import math

data=np.loadtxt("text.txt")

(mu, sigma) = norm.fit(data)
w=data.max()-data.min()
x=np.arange(data.min()-w*0.2,data.max()+w*0.2,w/50.0)
y = mlab.normpdf( x, mu, sigma)
plt.plot(x, y)
n, bins, patches = plt.hist(data, math.sqrt(data.size),normed=1)

plt.legend(['Normalna','Meritev'])
plt.xlabel('t (ms)')
plt.ylabel('verjetnost (1/ms)')
print mu,sigma, data.mean(), math.sqrt(data.var())
plt.show()

Nazaj na prejšnjo stran

---

3. Primer iskanja koeficientov premice z upoštevanjem napak

Skripta v pythonu poišče koeficiente premice ali drugega modela podanega v funkciji func. Nato poišče napake koeficientov. Podatki se nahajajo v datoteki podatki.txt v treh stolpcih. V prvem stolpcu je x, v drugem je y, v tretjem je napaka y. Vrednosti y in napake se nato še preračunajo na željene količine. Pri računanju napake upoštevamo pravilo za izračun napak.

from scipy import sqrt
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np

data = np.loadtxt("podatki.txt")
x = data[:, 0]
tlak = data[:, 1] #tlak bomo preracunali za vrednosti y
et = data[:, 2] #napaka meritve tlaka

#izracun izkoristka iz tlaka
y = (790 * 9.81 * 1.695) / (tlak * 1e5 * 1.695 * 0.002590)
ey = y / tlak * et  #izracun napake iz tlaka

#model - v tem primeru je premica z koeficienti a in b
def func(x, a, b):
    return a+b*x

#iskanje koeficientov z upostevanjem napake
fitpar,fitcov = curve_fit(func,xdata=x, ydata=y, sigma=ey)
print "presek:",fitpar[0],"+-",sqrt(fitcov[0,0])
print "naklon",fitpar[1],"+-",sqrt(fitcov[1,1])

#iskanje koeficientov brez upostevanja napake
#fitpar2,fitcov2 = curve_fit(func,xdata=x,ydata=y)
#print "brez upostevanja napak"
#print "presek:",fitpar2[0],"+-",sqrt(fitcov2[0,0])
#print "naklon",fitpar2[1],"+-",sqrt(fitcov2[1,1])

#matplotlib plotting
plt.errorbar(x, y, yerr=ey, fmt='go')
plt.plot(x, func(x, fitpar[0], fitpar[1]), '--')
plt.legend(['meritev 790kg', 'linearni model'])
plt.ylabel('izkoristek')
plt.xlabel('pretok (l/min)')
plt.axis([10, 40, 0.7, 1])
plt.show()

Nazaj na prejšnjo stran

---

4. Primer iskanja koeficientov kompleksnejšega modela

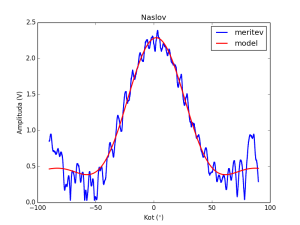
Skripta v pythonu poišče koeficiente modela podanega v funkciji func. Ker funkcija obdela celoten array v enem klicu in ker je problem ko je kot 0, moramo ročno preračunati vsako vrednost posebej. Nato poišče napake koeficientov. Podatki se nahajajo v datoteki podatki.txt v dveh stolpcih. V prvem stolpcu je x, v drugem je y.

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit
import math
data = np.loadtxt("podatki.txt",skiprows=3)
y = data[:,1]
x = data[:,0]

#model izracuna ga za vse elemente naenkrat                                     
def func(x, a, b, c,d):
    #problem is when x is zero division doesnt work                         
    arg = b * (x-d)
    ans = arg #make a copy                                                      
    for i in range(len(ans)): #calculate for each element 
        if arg[i] == 0.0: ans[i] = 1.0
        else: ans[i] = np.power(np.divide(np.sin(arg[i]),arg[i]),2)
    return a * ans + c

fitpar,fitcov = curve_fit(func,xdata=x, ydata=y)

print "parametri:",fitpar
print "napake:",np.sqrt(np.diag(fitcov))

plt.plot(x,y,linewidth=2.0)
plt.plot(x,func(x,fitpar[0],fitpar[1],fitpar[2],fitpar[3]),"r",linewidth=2.0)
plt.title("Naslov")
plt.xlabel(r'Kot ($\degree$)')
plt.ylabel("Amplituda (V)")
plt.legend(["meritev","model"])                                               
plt.show()

Nazaj na prejšnjo stran

---

Egon Pavlica, 21. maj 2014